The Trichromatic Lottery Ticket Hypothesis
[Japanese|English]
Abstract
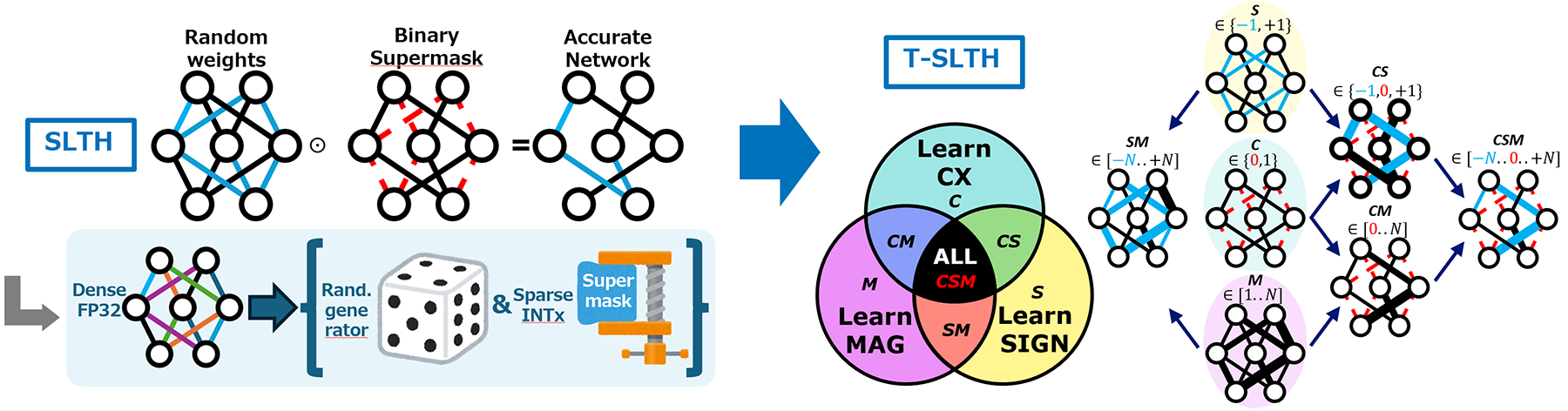
Pruning and quantization are common approaches in neural network compression. However, the Strong Lottery Ticket Hypothesis (SLTH) demonstrated that even before training, there exists a sparse subnetwork within a random initialization capable of achieving high accuracy. Instead of training the weights, a supermask is learned to determine active connections, allowing to reconstruct the network at inference time only from random seed and mask. Our research, the Trichromatic SLTH (T-SLTH), generalizes the SLTH into a new theoretical framework: trichromatic supermasks separately optimize three components of each weight—connectivity (C), sign(S), and magnitude scaling (M).
What makes it special?
- Arbitrary connectivity: Supports dense and random (arbitrary) structures that prior SLTH could not handle.
- Versatility: Potentially applicable across heterogeneous hardware substrates, from digital to photonic devices.
- Unified theoretical framework: Reinterprets all prior supermask variants as combinations trichromatic masks.
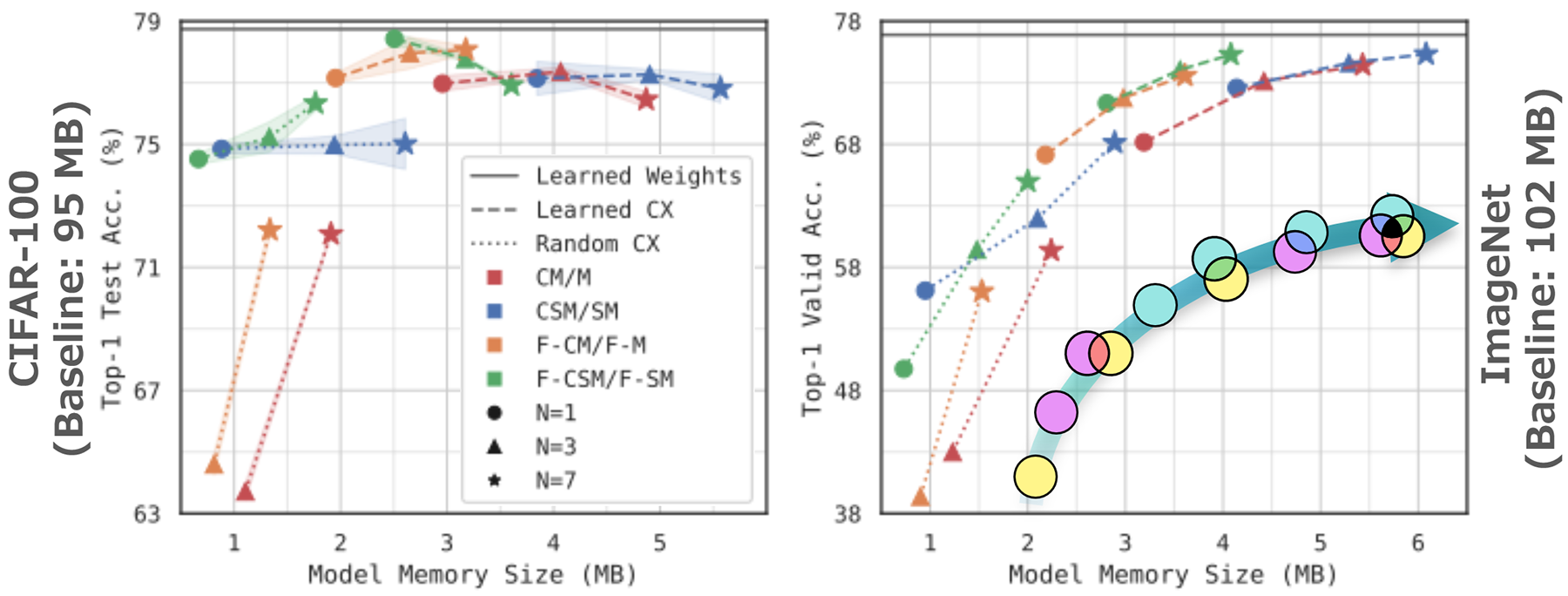
- Compression performance: Compresses ResNet-50 on CIFAR-100 ×38 (2.51 MB) while maintaining 78.43% accuracy, and achieves 75.28% on ImageNet at 4.1 MB.
- New perspective: Revisits the assumption that “connectivity is all that matters,” bridging with quantization-aware training (QAT) and compression.
Experimental results
- CIFAR-100: ResNet-50 achieves 78.43% accuracy with 38× compression (2.51 MB).
- ImageNet: 75.28% accuracy with 25× compression (4.1 MB).
- Arbitrary connectivity validation: Demonstrated stable performance not only in sparse models, but also in densely connected and partially random structures.
Future work
T-SLTH provides a unified theoretical foundation spanning pruning, quantization, and randomness. Future work aims to apply this framework to heterogeneous hardware (optical, analog, quantum) and to develop compression methods leveraging structural priors. Ultimately, this line of research seeks algorithm–hardware co-design for energy efficiency.
Publications
- Á. López García-Arias, Y. Okoshi, H. Otsuka, D. Chijiwa, Y. Fujiwara, S. Takeuchi, M. Motomura, “The Trichromatic Strong Lottery Ticket Hypothesis: Neural Compression With Three Primary Supermasks,“ Workshop on Machine Learning and Compression, NeurIPS, 2024. (Spotlight).
https://openreview.net/pdf?id=CfI2KfPb4C
Contact
Ángel López García-Arias
Recognition Research Group, Media Information Laboratory, NTT Communication Science Laboratories
Related Research
- Theoretical Understanding of Source-free Domain Adaptation
- Deep Image Generation Based on Optics and Physics
- Controlling the Color Appearance of Objects by Optimizing the Illumination Spectrum
- The Trichromatic Lottery Ticket Hypothesis
- Efficient Algorithm for K-Multiple-Means
- Unsupervised Learning of 3D Representations from 2D images
- Generalized Domain Adaptation
- Efficient Algorithm for Anchor Graph Hashing
- Zero-shot knowledge distillation
- Human pose estimation with acoustic signals