Efficient Algorithm for K-Multiple-Means
[Japanese|English]
Abstract
K-Means is a well-known clustering method for multidimensional data. However, since it assigns each data point to the nearest representative point, it is difficult to extract clusters with complex shapes. To address this issue, K-Multiple-Means was proposed. This approach can effectively extract complex-shaped clusters by grouping multiple sub-clusters. However, it suffers from the problem of high computational cost for clustering. We have developed an approach that enables fast clustering with K-Multiple-Means, even for large-scale datasets.
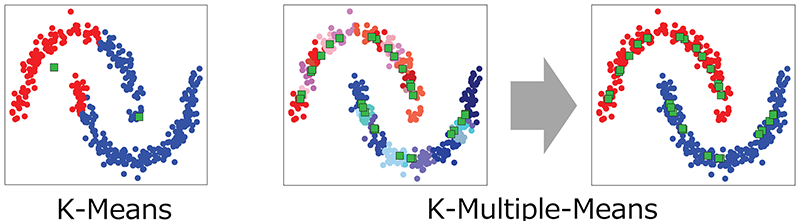
Contributions
K-Multiple-Means performs sub-cluster grouping by repeatedly computing distances between cluster centers and data points and then partitioning a bipartite graph. However, since this requires computing SVD of the matrix representing the bipartite graph, the computational cost becomes high.
We accelerates clustering by exploiting the connected components of the graph between the centers to construct a small block matrix, and then efficiently computing the SVD from the matrix.
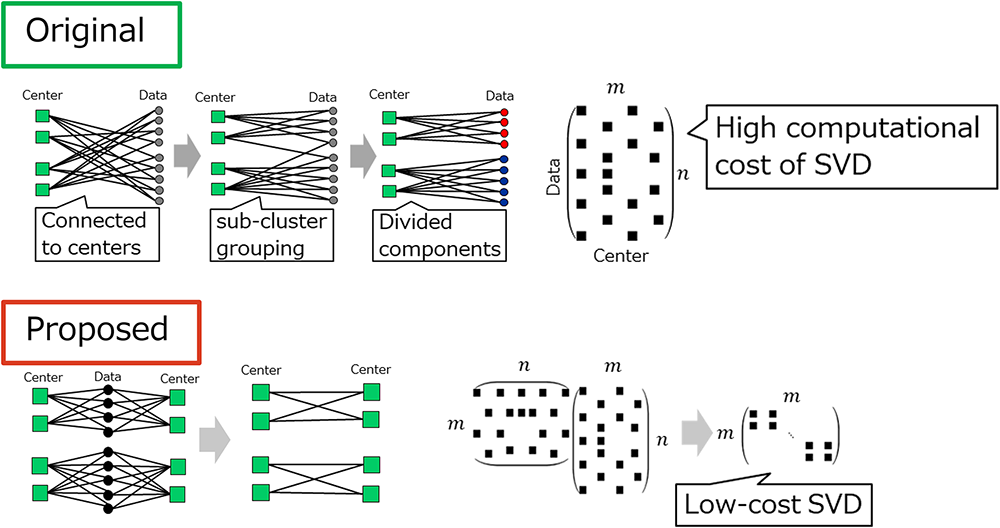
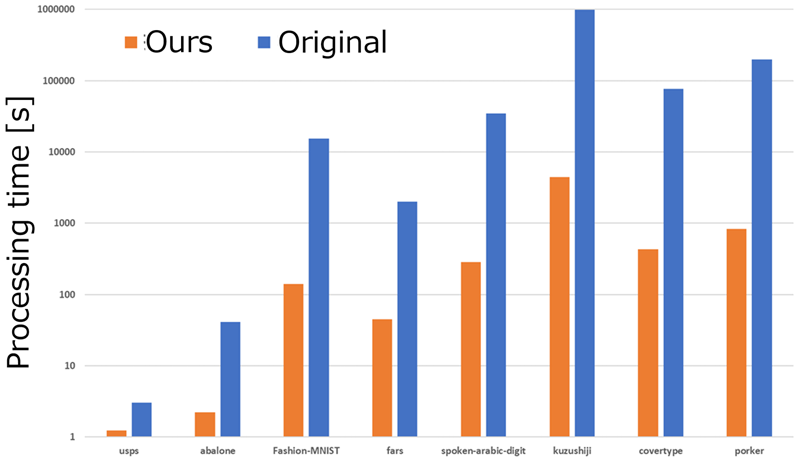
Experimental results
Our approach can perform clustering up to more than 230 times faster than the original K-Multiple-Means. For example, while the original method required more than 10 days to complete clustering on a dataset, our approach can accomplish it in about one hour.
Future work
Our approach accelerates K-Multiple-Means without sacrificing the quality of clustering results. K-Multiple-Means can be applied to a variety of tasks, including blind source separation, image segmentation, and network load balancing. Our approach is expected to serve as a breakthrough that enables these applications to be executed efficiently even on large-scale datasets.
Publications
- Fujiwara, Kumagai, Ida, Nakano, Nakatsuji, Kimura, “Efficient Algorithm for K-Multiple-Means”, Proc. ACM Manag. Data 2(1) (2024).
https://dl.acm.org/doi/pdf/10.1145/3639273
Contact
Yasuhiro Fujiwara
Recognition Research Group, Media Information Laboratory, NTT Communication Science Laboratories
Related Research
- Theoretical Understanding of Source-free Domain Adaptation
- Deep Image Generation Based on Optics and Physics
- Controlling the Color Appearance of Objects by Optimizing the Illumination Spectrum
- The Trichromatic Lottery Ticket Hypothesis
- Efficient Algorithm for K-Multiple-Means
- Unsupervised Learning of 3D Representations from 2D images
- Generalized Domain Adaptation
- Efficient Algorithm for Anchor Graph Hashing
- Zero-shot knowledge distillation
- Human pose estimation with acoustic signals