フォーマルメソッドによるセキュリティ検証手法
[Japanese|English]
ネットワークサービスの安全性を数学的な厳密さで保証する技術
インターネット上で投票やショッピングなどのサービスを安心して利用するためには、安全性の十分な確保が不可欠です。そのためには、これらネットワークサービスで用いられるプロトコル(通信手順)が、重要な情報を漏洩させないことや、なりすまし攻撃を防げることなど、さまざまなセキュリティ要件を満たしていることを検証する必要があります。しかし、高度な暗号技術を駆使した複雑なプロトコルの検証では、しばしば誤りやチェック洩れなどが起こります。
わたしたちは、フォーマルメソッドを用いて、セキュリティの検証を行う技術について研究しています。フォーマルメソッドとは、数学や数理論理学の蓄積を利用して、情報システムの正しさを厳密に検証するための手法です。これを暗号プロトコルに適用することで、ネットワークサービスのより高度な安全性を保証できるようになります。
わたしたちがめざすもの
フォーマルメソッドを、あらゆるシステムのさまざまなセキュリティ要件へ適用可能にするため、わたしたちは 2 つの方向性で研究を進めています。
[より複雑な性質を検証]
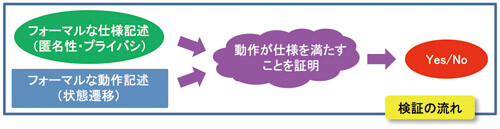
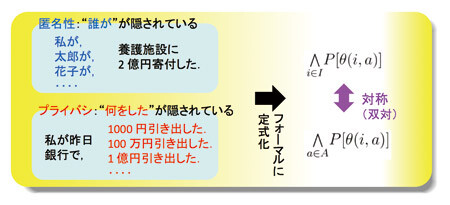
フォーマルメソッドで安全性要件を検証するためには、まずその要件・性質をフォーマルに記述する必要があります。秘匿性(クレジットカード番号を漏らさない、など)や認証性など(なりすましを防ぐ)性質が単純な場合は問題になりませんが、より複雑な性質、たとえば匿名性(だれがオバマに投票したかわからない)やプライバシ(センサなどによって不当に行動監視されない)などに検証対象を広げる場合、その記述・定式化そのものが問題となります。
[より高精度な検証]
フォーマルメソッドによる安全性検証では、定理証明系やモデル検査系などのツールを用いて、厳密かつ機械的なプロトコル検証を可能にしています。しかし自動化のために暗号系に関する仮定を、理想化・単純化(破られる確率はゼロ、など)しなければならないため、精度が低いという欠点がありました。近年、この仮定を現実に近づけることでより高精度化する研究が、世界的に活性化しています。
匿名性・プライバシのフォーマルメソッド
わたしたちは、匿名性・プライバシを、行為者と行為内容の結び付きに関する情報の隠蔽ととらえ、フォーマルに定式化し検証する手法を考案しました。このようなとらえ方では、匿名性とプライバシは互いに対称な性質(数学では双対と呼ばれる)となります。この対称性は、検証要件の定式化に明快なパースペクティブをあたえるとともに、検証作業の効率化にも役立つことがわかりました。具体的なプロトコルとして、FOO(藤岡・岡本・太田によって1992年に考案された、大規模インターネット電子投票プロトコル)の匿名性・プライバシ検証に成功しています。
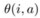 : “i さんが a をした”という、人と行為の結びつきのフォーマルな表現。
: “i さんが a をした”という、人と行為の結びつきのフォーマルな表現。ハッシュ関数を用いたプロトコルの高精度検証
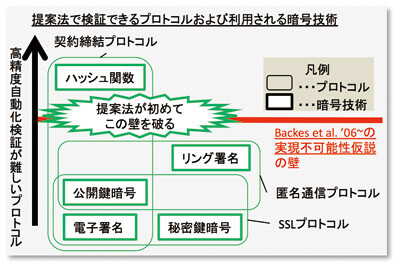
従来、安全性解析に対するアプローチは、暗号学とフォーマルメソッドでは異なっていました。暗号学者は、(確率は低いが)暗号は解読される可能性があるという現実的仮定のもとで解析を行います。一方フォーマルメソッドでは、検証の自動化のために暗号は絶対に解読されないという仮定をおいており、そのことで検証の精度が犠牲になっていました。近年、この仮定をより現実に近づけることで検証を高精度化する研究が、世界的に活性化しています。
わたしたちは、現実的な仮定のもとでフォーマルに扱うことが不可能とされていたハッシュ関数を用いたプロトコルを、高精度かつ自動的に検証する手法を考案しました。