離散構造アルゴリズム
計算機が取り扱う対象の多くは、離散的な構造を持っていると捉えることができます。集合や文字列はその代表例です。
我々は、離散的な構造を持つ対象に対しての効率的で実用的なアルゴリズムに対する研究を行っています。
特に、ゼロサプレス型二分決定グラフと呼ばれるデータ構造を用いることで、「条件を満たすすべての組合せ」を集合として保持することにより、所望の課題を解くことを中心に研究を進めています。
組合せの列挙
何かの条件を満たす組合せを計算機で取り扱う場合、条件を満たすすべての組合せを小さくデータベース化しておくことができれば、組み合わせを含む計算や検索に効率的に利用することができます。
我々はこういった組合せの中でも「厳密被覆」と呼ばれる組合せについて着目しました。厳密被問題とは、与えられたピースを隙間なく敷き詰める問題であり、現実世界では電子回路基板のモジュール配置や、マンションの部屋にの間取りに対応します。
従来法よりも最大10,000倍以上の高速化に成功し、たとえば12x12マスにテトロミノを敷き詰める問題では、敷き詰め方は13,664,822,582,333,502,156,627,512 通り存在することを世界で初めて見つけました。

ゲーム理論の均衡計算
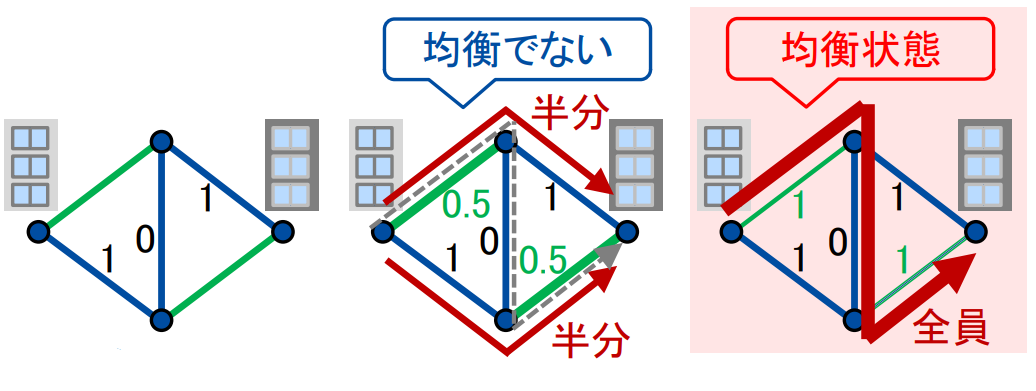
道路や通信網など、多数の人が同じ資源を共有利用する際の混雑の変化は、ゲーム理論の一種である「混雑ゲーム」としてとらえることができます。
混雑ゲームとして見た場合に、各利用者が誘導や制御がなく各々自分勝手にコストが小さい経路を選んだ際に、どこがどの程度混雑することになるのかは、混雑ゲームの均衡として求めることができます。
従来この均衡計算は小さなネットワークであっても計算時間が膨大で実質的には計算することはできませんでした。我々は二分決定グラフを用いて経路の集合を小さく表現することで、計算を高速化し、実用的な大きさのネットワークでの計算を可能にしました。
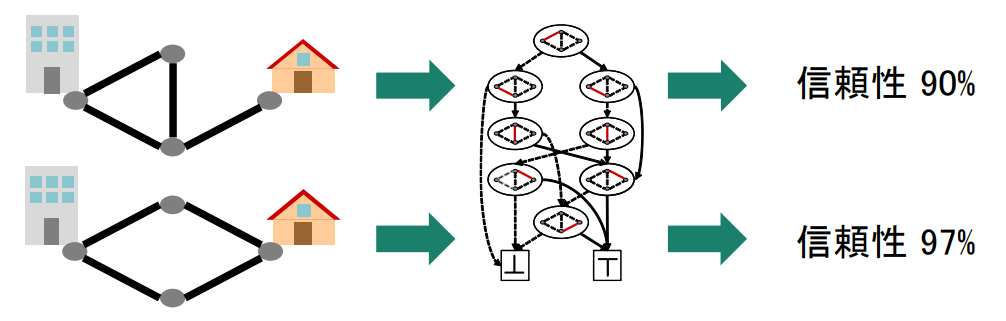
ネットワーク設計への応用
通信網や電力網などを増強する場合に、高めるべき指標のひとつとして「信頼性」が挙げられます。ネットワークの場合、個々の要素の信頼性を考えるだけでなく、ネットワーク全体としての信頼性を考える必要があります。しかし、ネットワーク全体での信頼性は膨大な組合せの計算を必要とするため厳密な信頼性の計算は困難でした。我々は、二分決定グラフ上のA*サーチという手法を考案し、この手法を用いて、定められた予算内で厳密に最も信頼性が高くなるようなネットワークの増強方法を見つけることを可能にしました。